Számolj a szöveggel!
Szöveges feladatok gyakorló 5-6. osztályosok számára
A különböző tantárgyak feladott szövegei fejfájást tudnak okozni, kiváltképp a matematikai szöveges feladatok megoldása. Erre a fejfájásra azonban csak egy gyógyszer van: értsük meg a feladat lényegét! Ehhez nyújtunk most segítséget új, 200 feladatos gyakorlónkkal! Kezdésként nézzük csak meg, mi a probléma gyökere!
Az alapvető meghatározás szerint matematikai szöveges feladatnak tekinthető minden olyan probléma, melynek megfogalmazása szöveges, és a megoldáshoz elengedhetetlen a matematika valamely területének alkalmazása. Ehhez pedig szükséges a matematika szövegesfeladat-megoldó képesség.
A matematikában elengedhetetlen például a számolási készség, a rendszerezés gondolkodási képessége, a problémamegoldás, nem utolsó sorban a figyelem, emlékezet és a feladatmegoldási sebesség. Azonban van még egy fontos elem: a szövegértés, szövegértelmezés, ami a kommunikációs képességhez tartozik, ezzel jelezve, hogy a számolás mellett alapvető az értelmezés módja is.
Miből következtethetünk arra, hogy a tanulók megértették egy matematikai feladat szövegét? Abból például, hogy:
- A feladattal összefüggő, önálló és értelmes kérdést tud feltenni.
- A feladatot saját szavaival el tudja mondani, pontosan vissza tudja idézni.
- A feladatot helyesen megoldja.
A megértésre azonban több nehezítő körülmény is hatást gyakorol, például a terjedelmes szöveg, a bonyolult, összetett mondatot tartalmazó szövegezés, vagy a matematikai fogalmak és összefüggések alkalmazása. Sok múlik azon, hogy egy vessző hova kerül, nézzük csak meg!
Rajzolj egy olyan négyszöget, amelynek van két derékszögnél nagyobb szöge!
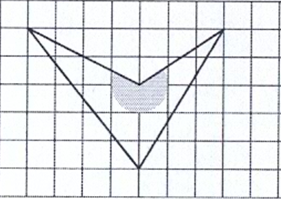
Rajzolj egy olyan négyszöget, amelynek van két, derékszögnél nagyobb szöge!
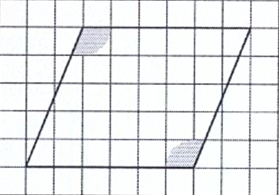
Látod a különbséget? Pedig csak egy vessző az eltérés, mégis teljesen más az eredmény!
A szövegezés világa minden egyes zugában tartogat részleteket, amiket be kell barangolni! Ezeket a részleteket pedig, mint egy kirakós játék, össze kell szedni és a végén kirakni, hogy teljes legyen a kép.
Nézzük meg, hogy történhet ez egy egyenes szövegezésű feladatnál!
Béla egy 6820 Ft-os tollasütőt és 3 tollaslabdát vásárolt. Mennyit fizetett összesen, ha egy tollaslabda 270 Ft-ba kerül?
Írjuk fel a „kirakós darabokat”:
Tollasütő ára: 6820 Ft
1 tollaslabda ára: 270 Ft
3 tollaslabda ára: 3 x 270 Ft = 810 Ft
Összesen: 6820 Ft + 810 Ft = 7630 Ft
Ilyen és ehhez hasonló gyakorlófeladatokkal készültünk!
Ha problémás a matematikai szövegértés 5-6. osztályos gyermeke számára, akkor 200 feladatos gyakorlónkkal megoldást talál! A Szöveges feladatok gyakorló különlegessége, hogy nem csupán feladatokat és megoldásokat tartalmaz, hanem a megoldások levezetésével könnyedén megérthető a feladat lényege, ezáltal a szöveges feladatok olvasás- és értelmezéstechnikája fejleszthető. Így tehát nemcsak az értelmezés kialakítására, hanem fejlesztésére is hangsúlyt fektettünk. Jól hangzik, ugye? Már nem kell sokat várni, jövő héten előrendelheti!